水塘抽样算法，正好今天的「每日一题」是考这个算法，不写个笔记记录下感觉又快忘完了。

Intro

说白了就是有点像时间换空间？在一段超长且长度未知的数据流中，如果需要以一个相同的概率去实时抽样，则需要用到该算法。
如果有一个数组 data ，需要随机跳出一个元素，我们之前都是通过 random.nextInt(data.length) 来得到这个元素的下标，从而得到该元素值。但是遇到需要在大小为 $n$ 的数组中有 $k$ 个值是相同的元素，需要以相同概率取出其中一个元素这样的问题，那就不得不先预处理，将这 $k$ 个值相同元素都放到另外的空间中，然后在调用 random 函数进行抽取。但如果是水塘抽样则可以做到像迭代器一样，随时可以停止，在前面的抽样的过程中，保证每个元素时被以相同的概率抽到。
该算法的核心就是数学公式，在一次遍历中，可以做到保证每个需要被取出的元素抽到的概率是 $\frac1k$ 。
简单来说就是判断 random.nextInt(cnt) == 0 该条件是否成立， cnt 等于当前加入抽奖池的个数，当 cnt 为 $1$ 时， 第一个元素被选中的概率是 $\frac11$ ；当 cnt 为 $2$ 时，第 $2$ 个元素被选中概率是 $\frac12$ ；当 cnt 为 $3$ 是，第 $3$ 个元素被选中概率是 $\frac13$ ；而且它并不会影响之前的元素是否被选中。当第 $k$ 个元素的概率是 $\frac1k$，而第 $1$ 个元素被选中的概率就等于 $\frac11 \times (1 - \frac12) \times (1 - \frac13) \times ··· \times (1 - \frac1k) = \frac1k$
所以每个元素被选中的概率都是 $\frac1k$。这样就完成了随机抽样，并且可以对持续的流进行抽样。

Problem Description

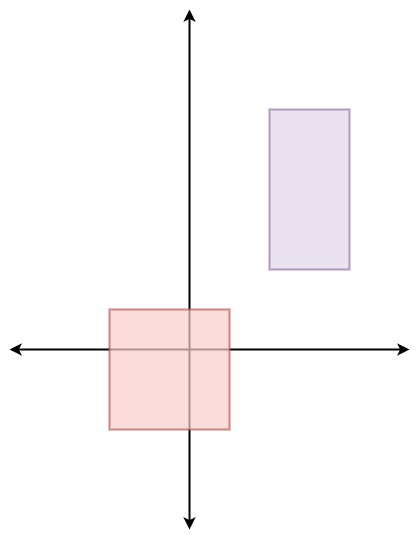
给定一个由非重叠的轴对齐矩形的数组 rects ，其中 rects[i] = [ai, bi, xi, yi] 表示 (ai, bi) 是第 i 个矩形的左下角点，(xi, yi) 是第 i 个矩形的右上角角点。设计一个算法来挑选一个随机整数点内的空间所覆盖的一个给定的矩形。矩形周长上的一个点包含在矩形覆盖的空间中。

在一个给定的矩形覆盖的空间内任何整数点都有可能被返回。

请注意 ，整数点是具有整数坐标的点。

实现 Solution 类:

• Solution(int[][] rects) 用给定的矩形数组 rects 初始化对象。
• int[] pick() 返回一个随机的整数点 [u, v] 在给定的矩形所覆盖的空间内。

note

• 1 <= rects.length <= 100
• rects[i].length == 4
• -109 <= ai < xi <= 109
• -109 <= bi < yi <= 109
• xi - ai <= 2000
• yi - bi <= 2000
• 所有的矩形不重叠。
• pick 最多被调用 104 次。

e.g.

1
2
3
4
5
6
7
8
9
10
11
12
13
14

输入: 
["Solution","pick","pick","pick","pick","pick"]
[[[[-2,-2,-1,-1],[1,0,3,0]]],[],[],[],[],[]]
输出: 
[null,[-1,-2],[2,0],[-2,-1],[3,0],[-2,-2]

解释：
Solution solution = new Solution([[-2, -2, 1, 1], [2, 2, 4, 6]]);
solution.pick(); // 返回 [1, -2]
solution.pick(); // 返回 [1, -1]
solution.pick(); // 返回 [-1, -2]
solution.pick(); // 返回 [-2, -2]
solution.pick(); // 返回 [0, 0]

Solution

只需要将所有点取出，利用 TreeSet 的堆排序类似二分查找随机到一个矩形，再对该矩形的 x, y 的最大最小值进行蓄水池抽样即可，注意边长上的点也是符合条件的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

class Solution {

    int max;
    int[][] rects;
    TreeMap<Integer, Integer> map;

    public Solution(int[][] rects) {
        int prev = 0;
        this.rects = rects;
        this.map = new TreeMap<>();
        for (int i = 0; i < rects.length; i++) {
            int curr = (rects[i][2] - rects[i][0] + 1) * (rects[i][3] - rects[i][1] + 1);
            map.put(curr + prev, i);
            prev += curr;
            this.max = prev;
        }
    }

    public int[] pick() {
        Map.Entry<Integer, Integer> e = map.higherEntry(new Random().nextInt(max));
        Integer idx = e.getValue();
        int[] rect = rects[idx];
        int x = 0;
        int y = 0;
        for (int i = rect[0]; i <= rect[2]; i++) {
            if (ThreadLocalRandom.current().nextInt(i - rect[0] + 1) == 0) {
                x = i;
            }
        }
        for (int i = rect[1]; i <= rect[3]; i++) {
            if (ThreadLocalRandom.current().nextInt(i - rect[1] + 1) == 0) {
                y = i;
            }
        }
        return new int[]{x, y};
    }
}

• Next Post →