Problem Description
在给定的网格中,每个单元格可以有以下三个值之一:
值 0 代表空单元格;
值 1 代表新鲜橘子;
值 2 代表腐烂的橘子。
每分钟,任何与腐烂的橘子(在 4 个正方向上)相邻的新鲜橘子都会腐烂。
返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回 -1。
note
1 <= grid.length <= 101 <= grid[0].length <= 10grid[i][j] 仅为 0、1 或 2
e.g.
示例 1:
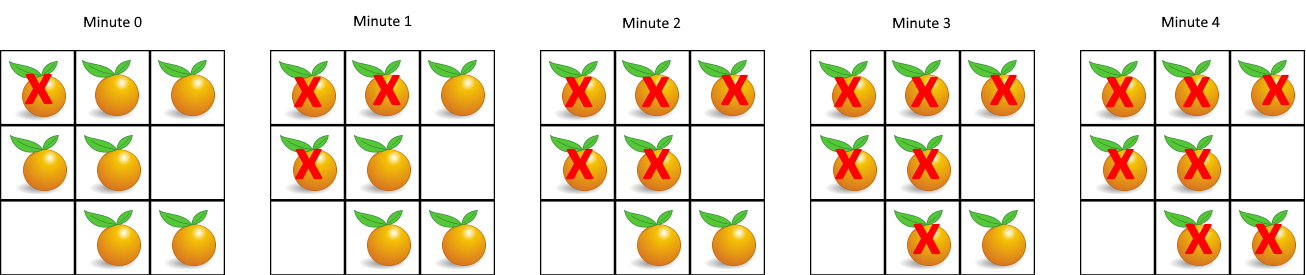
- 输入:
[[2, 1, 1],[1, 1, 0],[0, 1, 1]]
- 输出:
4
示例 2:
- 输入:
[[2, 1, 1],[0, 1, 1],[1, 0, 1]]
- 输出:
-1
示例 3:
Solution
网格、感染初一看就是深搜的题。
一分钟上下左右感染一个,感染的橘子又会上下左右感染邻近的新鲜的橘子,搁这生化危机呢。
每分钟感染周围(上下左右)的一排,那么用BFS走一走把所有的橘子感染一下(着色),求出最大深度max,然后正常遍历一下网格看还有没有新鲜橘子,有的话,return -1;没有的话return max。
一提交,GG了。
题目妹说只有一个「感染源」啊
如右边这种情况:[[2],[1],[1],[1],[2],[1],[1]]。它拥有2个「感染源」,最小分钟是2分钟,因为这2个「感染源」是同时作用邻近的新鲜橘子的。
那要怎么让多个起点同时遍历呢?
脑子里的第一个笨办法,就是先列举出所有的烂橘子,将每个烂橘子可达的所有点都遍历一遍然后着色,着什么色呢?分钟数。一个初始烂橘子的第一围的新鲜橘子被感染了,花费的时间是1分钟,然后这一围被感染的橘子成为了新的感染源,去感染其周围的新鲜橘子,下一轮的花费的时间还是1分钟,一共2分钟,将这个分钟数写到网格中,为了加以区分用负数表示。如:第一分钟被感染的新鲜橘子grid[x][y] = -1;第二分钟被感染的新鲜橘子grid[x][y] = -2。因为存在一个新鲜的橘子会被多个「感染源」感染的情况,所以一个新鲜的橘子的这个「感染分钟数」是多个,我们比较一下选最小的那个即可(在代码里是赋值比较大的,因为是负数)。
这样就完成了所有的新鲜的橘子,最快被感染的着色时间。我们常规遍历一遍,求出最大的那个时间就是总共花费的时间。如果网格中还存在新鲜的橘子,就直接return -1。
Java代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| public class Solution {
public int orangesRotting(int[][] grid) {
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] == 2) {
bfs(grid, i, j);
}
}
}
for (int[] ints : grid) {
for (int anInt : ints) {
if (anInt == 1) {
return -1;
}
}
}
int min = 0;
for (int[] ints : grid) {
for (int anInt : ints) {
min = Math.min(min, anInt);
}
}
return -min;
}
public void bfs(int[][] grid, int i, int j) {
boolean[][] visited = new boolean[grid.length][grid[0].length];
Queue<int[]> queue = new LinkedList<>();
queue.offer(new int[]{i, j});
visited[i][j] = true;
int depth = -1;
while (!queue.isEmpty()) {
int limit = queue.size();
depth++;
for (int k = 0; k < limit; k++) {
int[] xy = queue.poll();
int x = xy[0];
int y = xy[1];
visited[x][y] = true;
if (grid[x][y] < 0) {
grid[x][y] = Math.max(grid[x][y], -depth);
} else if (grid[x][y] == 1) {
grid[x][y] = -depth;
}
if (x - 1 >= 0 && !visited[x - 1][y] && grid[x - 1][y] != 2 && grid[x - 1][y] != 0) {
queue.add(new int[]{x - 1, y});
}
if (x + 1 < grid.length && !visited[x + 1][y] && grid[x + 1][y] != 2 && grid[x + 1][y] != 0) {
queue.add(new int[]{x + 1, y});
}
if (y - 1 >= 0 && !visited[x][y - 1] && grid[x][y - 1] != 2 && grid[x][y - 1] != 0) {
queue.add(new int[]{x, y - 1});
}
if (y + 1 < grid[0].length && !visited[x][y + 1] && grid[x][y + 1] != 2 && grid[x][y + 1] != 0) {
queue.add(new int[]{x, y + 1});
}
}
}
}
}
|
多源广度优先搜索
上面的的那个思路虽然可行,但是性能有点拉胯,因为一个格子被多次访问了。回到上面说的
那要怎么让多个起点同时遍历呢?
其实BFS模板一般只有一个初始节点,当把所有的烂橘子当做第一层,模拟同时感染周围的新鲜橘子,他的周围的新鲜的橘子就都是下一轮的目标了,都是同时的。所以事情就变得简单了起来。
其中特别注意一些特殊情况,例如只有烂橘子、只有好橘子;还有就是BFS图的遍历要特别注意visited访问标记要在加入到队列之后就要设置了。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
| class Solution {
public int orangesRotting(int[][] grid) {
boolean[][] visited = new boolean[grid.length][grid[0].length];
Queue<int[]> queue = new LinkedList<>();
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[i].length; j++) {
if (grid[i][j] == 2) {
queue.offer(new int[]{i, j});
visited[i][j] = true;
}
}
}
int depth = 0;
boolean flag = false;
while (!queue.isEmpty()) {
flag = true;
depth++;
int limit = queue.size();
for (int i = 0; i < limit; i++) {
int[] xy = queue.poll();
int x = xy[0];
int y = xy[1];
visited[x][y] = true;
if (grid[x][y] == 1) {
grid[x][y] = 2;
}
if (x - 1 >= 0 && !visited[x - 1][y] && grid[x - 1][y] == 1) {
queue.offer(new int[]{x - 1, y});
visited[x - 1][y] = true;
}
if (x + 1 < grid.length && !visited[x + 1][y] && grid[x + 1][y] == 1) {
queue.offer(new int[]{x + 1, y});
visited[x + 1][y] = true;
}
if (y - 1 >= 0 && !visited[x][y - 1] && grid[x][y - 1] == 1) {
queue.offer(new int[]{x, y - 1});
visited[x][y - 1] = true;
}
if (y + 1 < grid[0].length && !visited[x][y + 1] && grid[x][y + 1] == 1) {
queue.offer(new int[]{x, y + 1});
visited[x][y + 1] = true;
}
}
}
for (int[] ints : grid) {
for (int anInt : ints) {
if (anInt == 1) {
return -1;
}
}
}
return flag ? depth - 1 : depth;
}
}
|
