Intro

首先，树状数组的应用场景在哪里呢？这里摘抄三叶姐题解中的一段：

针对不同的题目，我们有不同的方案可以选择（假设我们有一个数组）：

数组不变，求区间和：「前缀和」、「树状数组」、「线段树」
多次修改某个数（单点），求区间和：「树状数组」、「线段树」
多次修改某个区间，输出最终结果：「差分」
多次修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间范围大小）
多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间范围大小）

作者：宫水三叶

看起来说前缀和搞不定的可以用树状数组来解决。

那么，树状数组是一种什么样的结构呢？首先它本身还是数组，不是像二叉树、字典树那样真正意义上的树了。因为没有必要做成那样的数据结构，它本身就是利用二进制的特性的来实现查询和更新操作的，数组结构已经完成可以满足分块处理的需求（太强了）。

假设有一个数组 arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ,11, 12, 13, 14, 15, 16}，那么树状数组 tree 在实际的结构中可能存储的是如下的数据：

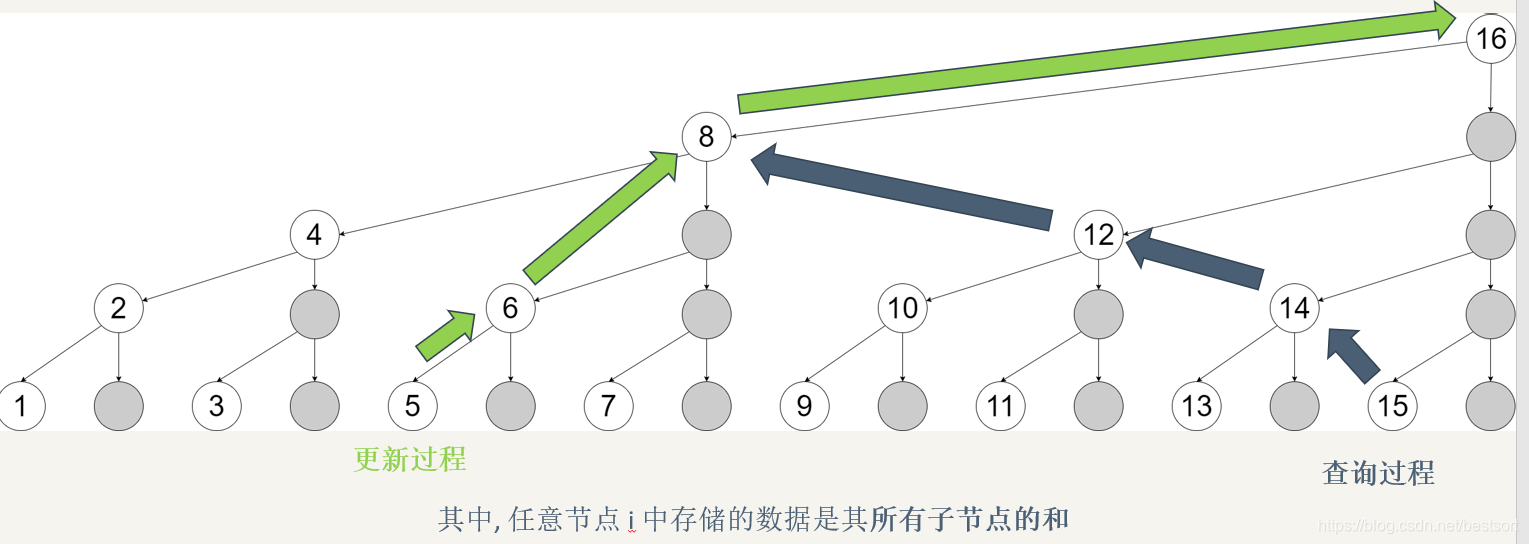
他看来还是像一颗二叉树，其中（下标从 1 开始）

tree[1] = arr[1]
tree[2] = arr[1] + arr[2]
tree[3] = arr[3]
tree[4] = tree[2] + tree[3] + arr[4] = arr[1] + arr[2] + arr[3] + arr[4]
…

简单理解 tree[i] 就等于其子节点的和再加上对应数组坐标的值。那么这个结构能够帮助我们做什么呢？前面我们提到了树状数组本身就是利用二进制的特性。其中这里有个算法 lowbit(int x)，用于取出 x 的最低位 1。

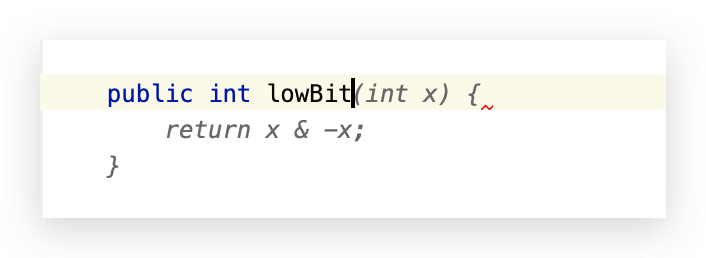
比如 $9$ 的二进制是 $1001$，他的 lowbit 就是 $1$，$10$ 的二进制是 $1010$，他的 lowbit 就是 $10$ 也就是 $2$。他的算法如下：

1
2
3

public int lowbit(int x) {
    return x & -x;
}

我在 Intellij IDEA 中打了一个类名，GitHub 的 Copilot 就马上就帮我自动补全这个算法了。。

如果有一个前缀和的数组 a，我们求 $l$ 到 $r$ 的区间怎么求呢？答案一般会是 a[r] - a[l - 1] (l >= 1) 或者 a[r + 1] - a[l] 之类的，其实树状数组也是利用 lowbit 算了个前缀和，但是它的时间复杂度不是 $O(n)$，而是 $O(logn)$。

假如现在要做一个更新操作，将 $idx$ 为 $5$ 的位置更新成 $val$，如果是前缀和数组，就需要从 $5$ 到 $16$ 区间的所有前缀和都更新一遍，但是对于树状数组来说，它的过程就是如图上所示只需要把 $5、6、8、16$ 这些节点更新了就行，因为他们的值都是由 $5$ 累加得到的。两者的代码:

public void _updateByPre(int idx, int val) {
    for (int i = idx; i < tree.length; i++) {
        tree[i] += val - arr[i];
    }
}
public void _updateByBinaryIndexedTree(int idx, int val) {
    for (int i = idx; i < tree.length; i += lowbit(i)) {
        tree[i] += val - arr[i];
    }
}

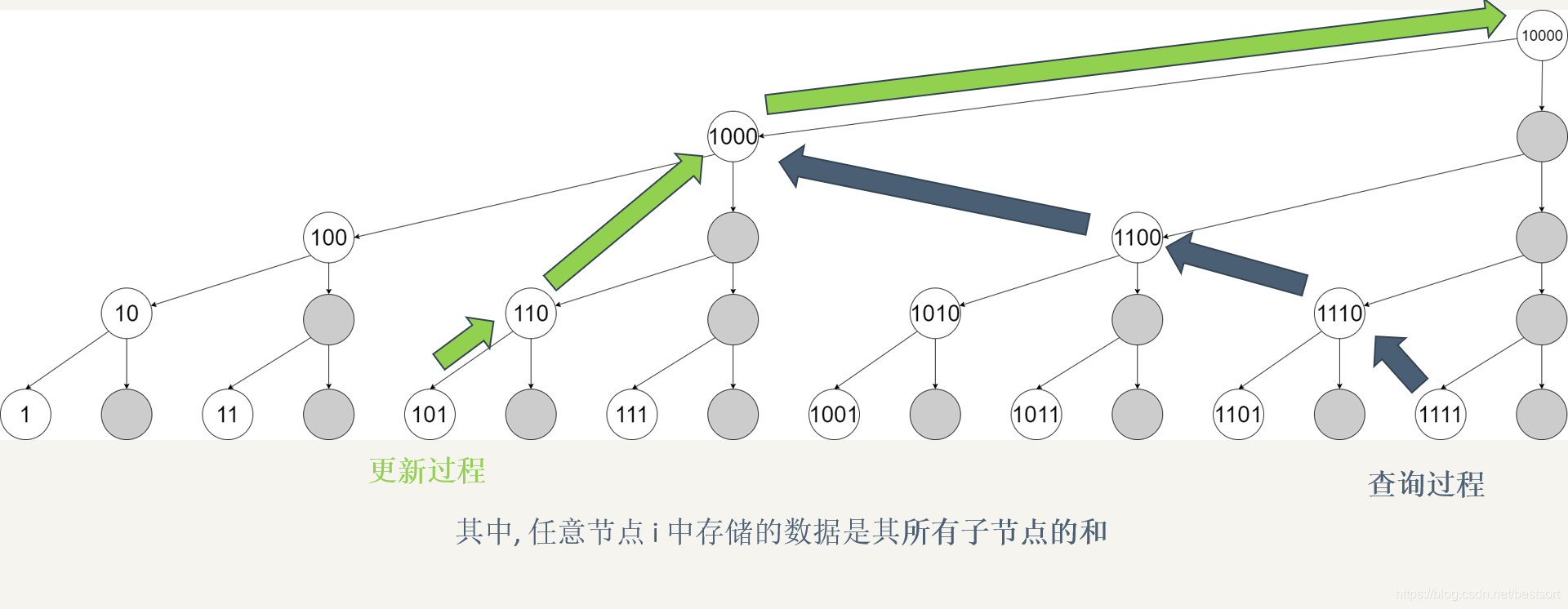
如果是查询呢？假设我想查找 $idx = 15$ 的前缀和，对于前缀和数组可以在 $O(1)$ 的情况下直接得到结果，而树状数组还是得需要 $O(logn)$ 的时间复杂度。树状数组需要把 $15、14、12、8$ 这些节点的值都加起来才能得到 $idx = 15$ 的前缀和。两者的代码：

public int _queryByPre(int idx) {
    return tree[idx];
}
public int _queryByBinaryIndexedTree(int idx) {
    int sum = 0;
    for (int i = idx; i >= 0; i -= lowbit(i)) {
        sum += tree[i];
    }
    return sum;
}

应用在题目中，求区间的和树状数组怎么做呢？那就是查找到两个端点的前缀和然后相减。树状数组模板代码：

package 默认模板;

import java.util.Arrays;

/**
 * @author <a href="https://github.com/Matthew-Han">Matthew Han</a>
 * @date 2022/4/7 16:03 07
 * @since 1.0
 **/
public class BinaryIndexedTree {

    int[] tree;

    public BinaryIndexedTree(int[] arr) {
        this.tree = new int[arr.length + 1];
        for (int i = 0; i < arr.length; i++) {
            update(i + 1, arr[i]);
        }
    }

    public void update(int idx, int delta) {
        for (int i = idx; i < tree.length; i += lowBit(i)) {
            tree[i] += delta;
        }
    }

    public int query(int idx) {
        int res = 0;
        for (int i = idx; i > 0; i -= lowBit(i)) {
            res += tree[i];
        }
        return res;
    }

    public int query(int left, int right) {
        return query(right + 1) - query(left);
    }

    public int lowBit(int x) {
        return x & -x;
    }

    @Override
    public String toString() {
        return Arrays.toString(tree);
    }

}

利用 update 方法完成对原始数组初始化前缀和相加，其中注意不能从 0 开始，不然会无限循环，因为 lowBit(0) = 0。

Problem Description

给你一个数组 nums ，请你完成两类查询。

其中一类查询要求更新数组 nums 下标对应的值
另一类查询要求返回数组 nums 中索引 left 和索引 right 之间（包含）的 nums 元素的和，其中 left <= right

实现 NumArray 类：

NumArray(int[] nums) 用整数数组 nums 初始化对象
void update(int index, int val) 将 nums[index] 的值更新为 val
int sumRange(int left, int right) 返回数组 nums 中索引 left 和索引 right 之间（包含）的 nums 元素的和（即，nums[left] + nums[left + 1], ..., nums[right]）

note

1 <= nums.length <= 3 * 104
-100 <= nums[i] <= 100
0 <= index < nums.length
-100 <= val <= 100
0 <= left <= right < nums.length
调用 update 和 sumRange 方法次数不大于 3 * 104

e.g.

输入：
["NumArray", "sumRange", "update", "sumRange"]
[[[1, 3, 5]], [0, 2], [1, 2], [0, 2]]
输出：
[null, 9, null, 8]

解释：
NumArray numArray = new NumArray([1, 3, 5]);
numArray.sumRange(0, 2); // 返回 1 + 3 + 5 = 9
numArray.update(1, 2);   // nums = [1,2,5]
numArray.sumRange(0, 2); // 返回 1 + 2 + 5 = 8

Solution

树状数组可以在比较小的时间复杂度下解决这一题：#307 区域和检索 - 数组可修改

class NumArray {

    int[] nums;
    BinaryIndexedTree bit;

    public NumArray(int[] nums) {
        this.nums = nums;
        this.bit = new BinaryIndexedTree(nums);
    }

    public void update(int index, int val) {
        bit.update(index + 1, val - nums[index]);
        nums[index] = val;
    }

    public int sumRange(int left, int right) {
        return bit.query(left, right);
    }

}

数据结构：树状数组

树状数组？批状数组！

Intro

Problem Description

note

e.g.

Solution

CATALOG

FEATURED TAGS

FRIENDS