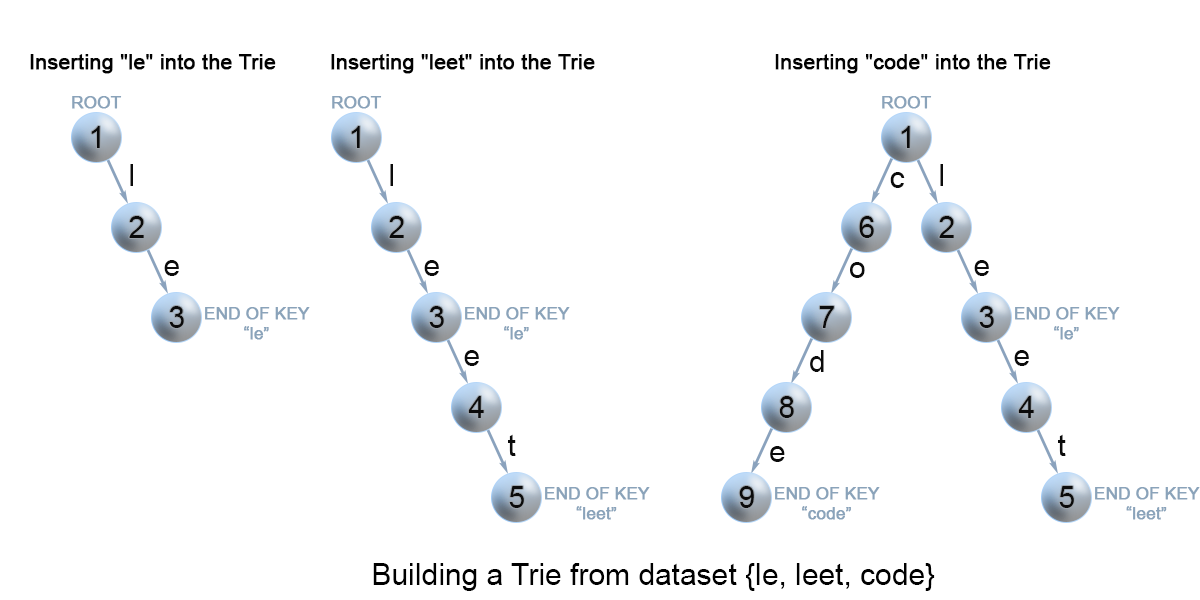
介绍

Trie (发音为 “try”) 或前缀树是一种树数据结构，用于检索字符串数据集中的键。这一高效的数据结构有多种应用：

自动补全

谷歌搜索建议
拼写检查

文字处理软件中的拼写检查
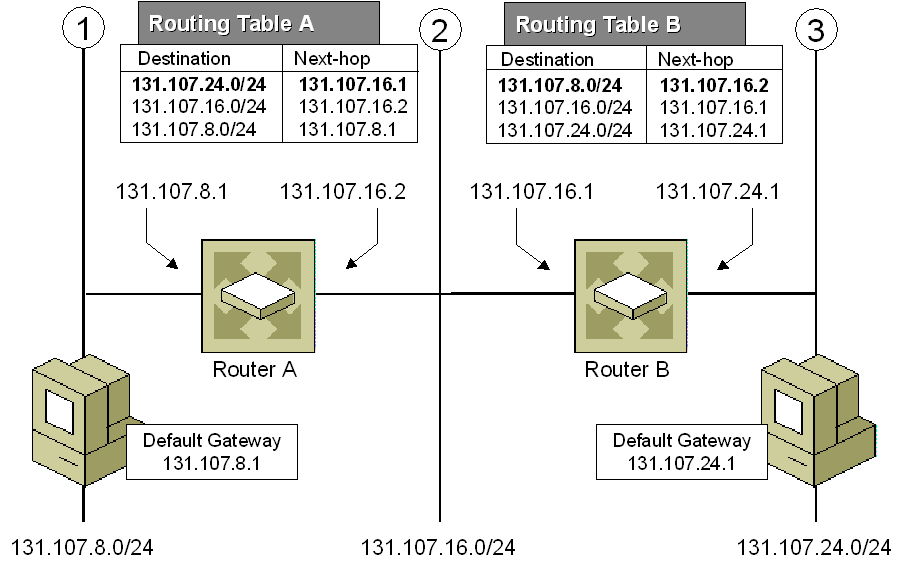
IP 路由 (最长前缀匹配)

使用Trie树的最长前缀匹配算法，Internet 协议（IP）路由中利用转发表选择路径
T9 (九宫格) 打字预测

T9（九宫格输入），在 20 世纪 90 年代常用于手机输入。
单词游戏

Trie 树可通过剪枝搜索空间来高效解决 Boggle 单词游戏

还有其他的数据结构，如平衡树和哈希表，使我们能够在字符串数据集中搜索单词。为什么我们还需要 Trie 树呢？尽管哈希表可以在 O(1) 时间内寻找键值，却无法高效的完成以下操作：

找到具有同一前缀的全部键值。
按词典序枚举字符串的数据集。

Trie 树优于哈希表的另一个理由是，随着哈希表大小增加，会出现大量的冲突，时间复杂度可能增加到 O(n)，其中 n 是插入的键的数量。与哈希表相比，Trie 树在存储多个具有相同前缀的键时可以使用较少的空间。此时 Trie 树只需要 O(m) 的时间复杂度，其中 m 为键长。而在平衡树中查找键值需要O(mlogn) 时间复杂度。

数据结构图

Problem Description

实现一个 Trie (前缀树)，包含 insert, search, 和 startsWith 这三个操作。

note

你可以假设所有的输入都是由小写字母 a-z 构成的。
保证所有输入均为非空字符串。

e.g.

Trie trie = new Trie();

trie.insert("apple");
trie.search("apple");   // 返回 true
trie.search("app");     // 返回 false
trie.startsWith("app"); // 返回 true
trie.insert("app");   
trie.search("app");     // 返回 true

Solution

利用前缀树就能很好的解决这一题 #208 实现 Trie (前缀树)。

首先构建一个前缀树的数据结构模型

static class TireTree {

    private boolean isEnd;
    private final TireTree[] data;
    private Character ele;
    private final static int CAPACITY = 26;

    public TireTree(char ele) {
        this.ele = ele;
        this.data = new TireTree[CAPACITY];
        this.isEnd = false;
    }

    @Override
    public String toString() {
        return "TireTree{" +
                "isEnd=" + isEnd +
                ", data=" + Arrays.toString(data) +
                ", ele=" + ele +
                '}';
    }
}

当然还可以扩展出set、get方法以供方便调用。

继续完善解决该题，难点在于insert方法，当插入某串字符串的子串时，需要将末尾节点的isEnd标记为置true；如果出现新的字符，需要插入一个新的节点。search方法只要递归判断末尾节点标记位是否为true即可，而startsWith只要递归判断prefix能否在该树下走完。

public class ImplementTriePrefixTreeII {

    static class TireTree {
      
        private boolean isEnd;
        private final TireTree[] data;
        private Character ele;
        private final int CAPACITY = 26;

        public TireTree(char ele) {
            this.ele = ele;
            data = new TireTree[CAPACITY];
            isEnd = false;
        }

        @Override
        public String toString() {
            return "TireTree{" +
                    "isEnd=" + isEnd +
                    ", data=" + Arrays.toString(data) +
                    ", ele=" + ele +
                    '}';
        }
    }

    TireTree tireTree;

    /**
     * #208 实现 Trie (前缀树)
     *
     * 执行用时： 37 ms , 在所有 Java 提交中击败了 99.72% 的用户
     * 内存消耗： 48.6 MB , 在所有 Java 提交中击败了 55.22% 的用户
     */
    public ImplementTriePrefixTreeII() {
        tireTree = new TireTree('$');
    }

    private void insert(TireTree tireTree, String target, int index) {
        if (index >= target.length()) {
            return;
        }
        char curr = target.charAt(index);
        TireTree currTree = tireTree.data[curr - 'a'];
        if (currTree == null) {
            tireTree.data[curr - 'a'] = new TireTree(curr);
            currTree = tireTree.data[curr - 'a'];
            currTree.ele = curr;
        }
        if (currTree.ele == curr && index == target.length() - 1) {
            currTree.isEnd = true;
            return;
        }
        insert(currTree, target, index + 1);
    }

    /**
     * 复合查询
     *
     * @param tireTree
     * @param target
     * @param index
     * @param isPrefix 是否是前缀查询
     * @return
     */
    private boolean search(TireTree tireTree, String target, int index, boolean isPrefix) {
        char curr = target.charAt(index);
        TireTree currTree = tireTree.data[curr - 'a'];
        if (currTree == null) {
            return false;
        } else {
            if (currTree.ele == curr) {
                if (index == target.length() - 1) {
                    return isPrefix || currTree.isEnd;
                } else {
                    return search(currTree, target, index + 1, isPrefix);
                }
            } else {
                return false;
            }
        }
    }

    /**
     * Inserts a word into the trie.
     */
    public void insert(String word) {
        TireTree tmp = tireTree;
        insert(tmp, word, 0);
    }

    /**
     * Returns if the word is in the trie.
     */
    public boolean search(String word) {
        TireTree tmp = tireTree;
        return search(tmp, word, 0, false);
    }

    /**
     * Returns if there is any word in the trie that starts with the given prefix.
     */
    public boolean startsWith(String prefix) {
        TireTree tmp = tireTree;
        return search(tmp, prefix, 0, true);
    }
  
}

数据结构：字典树

前缀树

介绍

数据结构图

Problem Description

note

e.g.

Solution

CATALOG

FEATURED TAGS

FRIENDS