数据结构 算法 leetcode 二叉搜索树 二叉树

LeetCode #378 有序矩阵中第K小的元素

#378 Kth Smallest Element in a Sorted Matrix

Posted by MatthewHan on 2020-08-16

Problem Description

给定一个 n x n 矩阵，其中每行和每列元素均按升序排序，找到矩阵中第 k 小的元素。
请注意，它是排序后的第 k 小元素，而不是第 k 个不同的元素。

note

你可以假设 k 的值永远是有效的，1 ≤ k ≤ n ^ 2

e.g.

  • 示例：

    1
    2
    3
    4
    5
    6
    7
    8
    matrix = [
       [1,  5,  9],
       [10, 11, 13],
       [12, 13, 15]
    ],
    k = 8,

    返回 13。

Solution

有一说一，被二维数组中的查找这道题整魔怔了。该题目的一种解法是将该矩阵模拟成一个二叉搜索树，利用其性质来做遍历方向的决策从而快速找到target。因为是模拟二叉搜索树，所以查找的时间复杂度是O(log(n ^ 2) )害挺快的。而这题也是同样的矩阵，但求的是第k个值（排序好的第K位）。

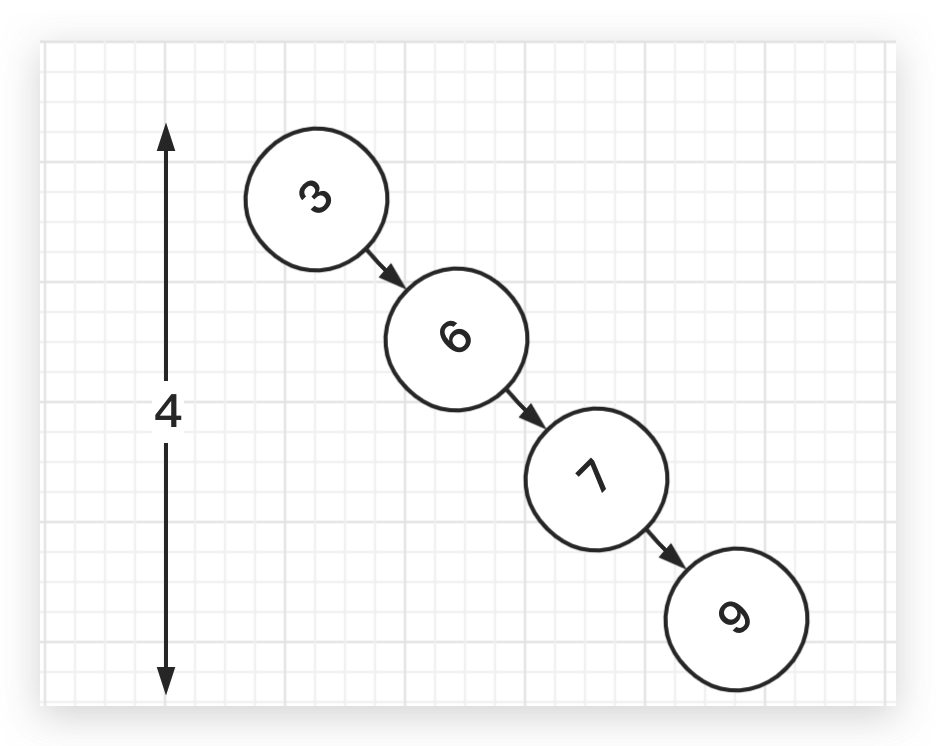
刚好晚上看了麻省理工公开课的其中一节课（二叉搜索树和快排）。认识到了二者相似性和奇妙之处。二叉搜索树的构建过程和快排的排序过程，二者在最坏的情况下时间复杂度都是O(n ^ 2) ，平均时间复杂度都是O(nlog(n) )，原理十分类似。BST在最差的情况是什么呢？就是像链表一样的情况，只有左节点或者右节点，这样它的高度就是节点数量（N），而在满二叉树下它的高度是（logN）。所以N个元素在构建BST的过程中，会先查找它应该在的位置（logN），N个元素就是O(nlog(n) )。但是在有序的数列（正、逆序）中会出现很糟糕的情况，这点和快排的pivot的选择很像。

像链表一样

所以这道题我就在想可不可以利用BST的中序遍历的结果来求第K个元素？该矩阵的特性很像BST，因为该矩阵的扁平成一维数组的结果对于构建BST应该是比较理想的，不可能出现上图的这种情况。

我的思路：

  1. 将矩阵遍历，添加到一个新数组中；
  2. 将该序列构建BST（新的序列对于构建BST是理想的）；
  3. 对该BST中序遍历，结果放在一个新数组中；
  4. 得到该新数组的第k个元素。

先将该矩阵的元素来构建一颗二叉搜索树。以下是二叉树模型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public class TreeNode {

    public int val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(int x) {
        val = x;
    }

    @Override
    public String toString() {
        return "TreeNode{" +
                "val=" + val +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
}

通过深度优先遍历的方式，对矩阵的右上角向左向下遍历，为了不出现重复访问，设置一个visited访问标记。类似先序遍历：

1
2
3
4
5
6
7
8
public static void dfs2(int[][] matrix, int x, int y, boolean[][] visited, List<Integer> res) {
    if (x >= 0 && y >= 0 && x < matrix.length && y < matrix[0].length && !visited[x][y]) {
        visited[x][y] = true;
        res.add(matrix[x][y]);
        dfs2(matrix, x - 1, y, visited, res);
        dfs2(matrix, x, y + 1, visited, res);
    }
}

接下来就是构建BST的过程代码辣：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static void buildBst(int n, TreeNode root) {
    if (n <= root.val) {
        if (root.left == null) {
            root.left = new TreeNode(n);
        } else {
            root = root.left;
            buildBst(n, root);
        }
    } else {
        if (root.right == null) {
            root.right = new TreeNode(n);
        } else {
            root = root.right;
            buildBst(n, root);
        }
    }

}

然后是对BST的中序遍历，BST的中序遍历打印的结果，一定是升序的。

1
2
3
4
5
6
7
public static void dfs(TreeNode root, List<Integer> res) {
    if (root != null) {
        dfs(root.left, res);
        res.add(root.val);
        dfs(root.right, res);
    }
}

其中要注意root节点在构建之前就已经创建了，所以第一个遍历的数组下标从1开始遍历，完整的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
public class KthSmallestElementInaSortedMatrix {
    public static int kthSmallest(int[][] matrix, int k) {
        List<Integer> tmp = new ArrayList<>();
        List<Integer> res = new ArrayList<>();

        boolean[][] visited = new boolean[matrix.length][matrix[0].length];
        dfs2(matrix, matrix.length - 1, 0, visited, tmp);
        TreeNode root = new TreeNode(tmp.get(0));
        // 第一位是root节点，已经add了
        for (int i = 1; i < tmp.size(); i++) {
            buildBst(tmp.get(i), root);
        }
        dfs(root, res);
        return res.get(k - 1);
    }

    public static void buildBst(int n, TreeNode root) {
        if (n <= root.val) {
            if (root.left == null) {
                root.left = new TreeNode(n);
            } else {
                root = root.left;
                buildBst(n, root);
            }
        } else {
            if (root.right == null) {
                root.right = new TreeNode(n);
            } else {
                root = root.right;
                buildBst(n, root);
            }
        }


    }

    public static void dfs(TreeNode root, List<Integer> res) {
        if (root != null) {
            dfs(root.left, res);
            res.add(root.val);
            dfs(root.right, res);
        }
    }

    public static void dfs2(int[][] matrix, int x, int y, boolean[][] visited, List<Integer> res) {
        if (x >= 0 && y >= 0 && x < matrix.length && y < matrix[0].length && !visited[x][y]) {
            visited[x][y] = true;
            res.add(matrix[x][y]);
            dfs2(matrix, x - 1, y, visited, res);
            dfs2(matrix, x, y + 1, visited, res);
        }
    }

}
class TreeNode {

    public int val;
    public TreeNode left;
    public TreeNode right;

    public TreeNode(int x) {
        val = x;
    }

    @Override
    public String toString() {
        return "TreeNode{" +
                "val=" + val +
                ", left=" + left +
                ", right=" + right +
                '}';
    }
}

最后，当然性能拉胯了。。这只是一种奇葩做法。。

CATALOG
    FEATURED TAGS
    数据结构 算法 leetcode 二叉搜索树 二叉树
    FRIENDS