Problem Description
在 N * N 的网格上,我们放置一些 1 * 1 * 1 的立方体。
每个值 v = grid[i][j] 表示 v 个正方体叠放在对应单元格 (i, j) 上。
请你返回最终形体的表面积。
note
1 <= N <= 500 <= grid[i][j] <= 50
e.g.
示例 1:
- 输入:
[[2]] - 输出:10
- 输入:
示例 2:
- 输入:
[[1,2],[3,4]] - 输出:34
- 输入:
示例 3:
- 输入:
[[1,0],[0,2]] - 输出:16
- 输入:
示例 4:
- 输入:
[[1,1,1],[1,0,1],[1,1,1]] - 输出:32
- 输入:
示例 5:
- 输入:
[[2, 2, 2], [2, 1, 2], [2, 2, 2]] - 输出:46
- 输入:
Solution
这题是#883 三维形体投影面积的升级版几何题目,883这题描述的利用一个二维数组的元素代表单个单元格的高度按照从左向右的顺序在xy平面上从上到下堆叠,求xy、yz、xz三个投影面积。
883这题相对简单,投影面积就是求最大值,因为矮的会被高的「覆盖」,只要求三个面即可。
示例图:
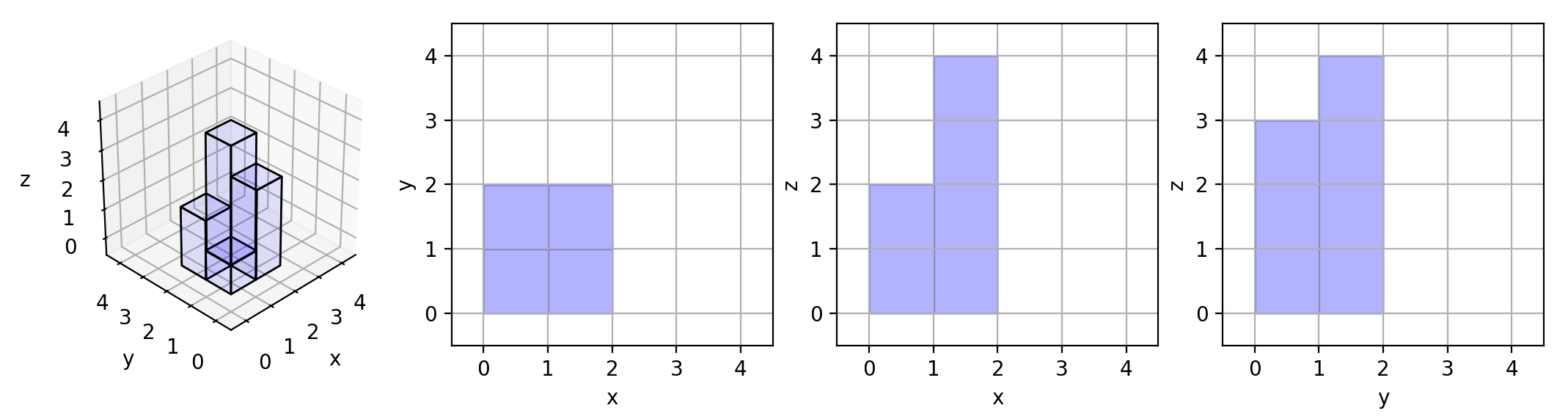
但是889这题就复杂了很多,他需要的是整个形体的表面积,而非投影面积。于是就带来了一个问题,被挡住的柱状形体可能存在表面积。
一开始我思考的是按照883的方式,还是先求出6个面(整个形体)的投影面积,再加上「凹陷」的表面积即可。因为只有存在「凹陷」情况,才会多出一部分表面积,但是所谓的“正证法”,会遇到的情况就十分多样了。
比如:
[[1, 0, 1]]和[1, 0, 0, 1][[1, 0], [0, 2]]
当凹陷是2个单位时或者0的情况等等这些情况就比较复杂,凹陷的判断十分的纷繁凌乱,感觉这个办法就很蠢。
在题解中看到了一个“阿姨”的方法,属实8错。他的思路是把所有柱子作为一个单位,求出所有柱子的表面积,如:1的表面积是1 * 4 + 2为6,2的表面积是2 * 4 + 2为10,再减去柱子与柱子之间相贴的面积。
给阿姨倒一杯卡布奇诺。

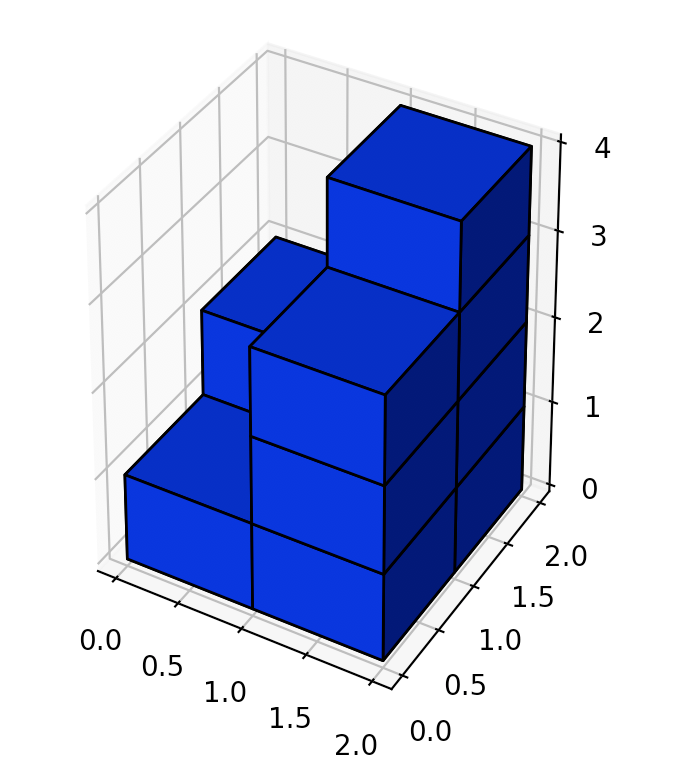
所以,当我们遍历整个形体时,只要判断该柱子与「上面」和「左边」是否有接触,有接触且不为0(为0,即柱子不存在,也不会出现遮挡的情况)的话,就减去较矮的那个柱子的高度 * 2,因为是两面相贴,所以要乘以2。
Java代码如下:
1 | public static int surfaceAreaPro(int[][] grid) { |
另外说明一点,这样写更简洁,但是效率还可以提升,提升在哪呢?因为当前柱子高度为0的时候,直接跳过即可。可是如上这样写即使当前柱子高度为0,①②③这三步都会走一遍会影响效率,但是看起来更简洁就vans了。